Monte Carlo simulation is widely used in finance to model the uncertainty and risk associated with investment portfolios. By generating thousands of random scenarios for asset prices, interest rates, or market returns, this technique helps quantify potential outcomes and their probabilities. For example, a portfolio manager can simulate future stock price movements over a year to estimate the probability of achieving a target return or facing a loss. In risk management, Monte Carlo methods assist in calculating Value at Risk (VaR) by simulating thousands of possible portfolio value paths under varying market conditions. This approach provides detailed insights into the distribution of possible losses and helps institutions comply with regulatory capital requirements. Financial analysts also apply Monte Carlo simulations to price complex derivatives by modeling the stochastic processes underlying asset prices.
Table of Comparison
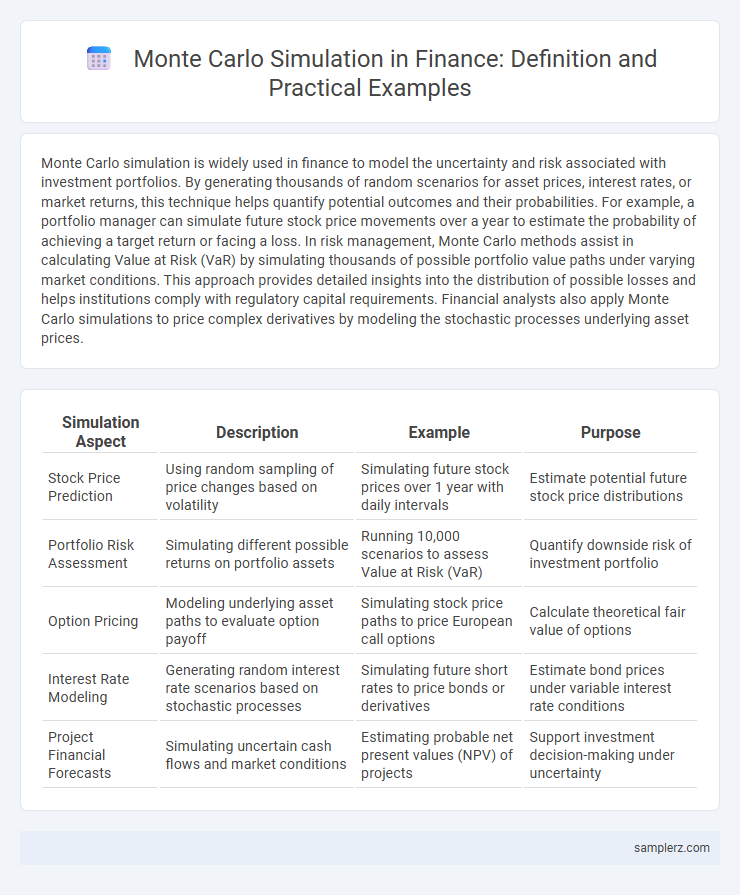
| Simulation Aspect | Description | Example | Purpose |
|---|---|---|---|
| Stock Price Prediction | Using random sampling of price changes based on volatility | Simulating future stock prices over 1 year with daily intervals | Estimate potential future stock price distributions |
| Portfolio Risk Assessment | Simulating different possible returns on portfolio assets | Running 10,000 scenarios to assess Value at Risk (VaR) | Quantify downside risk of investment portfolio |
| Option Pricing | Modeling underlying asset paths to evaluate option payoff | Simulating stock price paths to price European call options | Calculate theoretical fair value of options |
| Interest Rate Modeling | Generating random interest rate scenarios based on stochastic processes | Simulating future short rates to price bonds or derivatives | Estimate bond prices under variable interest rate conditions |
| Project Financial Forecasts | Simulating uncertain cash flows and market conditions | Estimating probable net present values (NPV) of projects | Support investment decision-making under uncertainty |
Introduction to Monte Carlo Simulation in Finance
Monte Carlo simulation in finance uses probabilistic models to assess the impact of risk and uncertainty on investment portfolios and asset prices. By generating thousands of random outcomes based on historical volatility and price distributions, it enables accurate forecasting of potential returns and Value at Risk (VaR). This technique enhances decision-making under uncertainty by quantifying the likelihood of various financial scenarios, including stock price fluctuations and interest rate changes.
Key Principles of Monte Carlo Methods
Monte Carlo methods in finance rely on random sampling and statistical modeling to simulate a wide array of possible outcomes for asset prices or portfolio returns, reflecting market volatility and uncertainty. Key principles include the generation of numerous random paths based on probability distributions, ensuring convergence to accurate estimates through law of large numbers, and applying risk-neutral measures to price derivatives under stochastic processes. These simulations provide quantitative insights for option pricing, risk management, and portfolio optimization by capturing complex market behaviors beyond analytical solutions.
Monte Carlo Simulation for Stock Price Forecasting
Monte Carlo Simulation for stock price forecasting involves generating thousands of potential future price paths by modeling the stock's volatility and drift based on historical data and stochastic processes such as Geometric Brownian Motion. This technique captures the uncertainty and randomness inherent in financial markets, providing probabilistic estimates of future stock prices rather than single-point predictions. Investors and risk managers use these simulations to assess potential outcomes, evaluate portfolio risk, and make informed decisions under conditions of market volatility.
Portfolio Risk Analysis Using Monte Carlo
Portfolio risk analysis using Monte Carlo simulation involves generating thousands of random scenarios for asset returns based on their statistical properties to estimate potential portfolio losses and gains. By modeling correlations between assets and incorporating volatility, this technique provides a probabilistic distribution of portfolio outcomes, enabling more accurate Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) assessments. Financial analysts use these simulations to optimize asset allocation, stress-test portfolios under adverse market conditions, and enhance decision-making under uncertainty.
Valuing Options with Monte Carlo Techniques
Monte Carlo simulation plays a crucial role in valuing complex financial options by generating numerous random price paths for the underlying asset, helping capture the stochastic nature of market conditions. This technique estimates the expected payoff of options by averaging discounted cash flows across simulated scenarios, accommodating path-dependent features and early exercise possibilities. Monte Carlo methods excel in pricing exotic options such as Asian options, barrier options, and American options where closed-form solutions are unavailable or insufficient.
Simulating Interest Rate Movements
Monte Carlo simulation models interest rate movements by generating thousands of possible future paths based on stochastic processes like the Vasicek or Cox-Ingersoll-Ross models. This approach captures the uncertainty and volatility in interest rate changes over time, helping to price interest rate derivatives and assess risk in bond portfolios. Financial institutions rely on these simulations for scenario analysis and stress testing to optimize asset-liability management strategies.
Credit Risk Assessment via Monte Carlo
Monte Carlo simulation in credit risk assessment models the probability of default by generating thousands of random scenarios to evaluate potential losses in loan portfolios. This approach quantifies credit exposure under varying economic conditions, incorporating factors such as borrower credit scores, interest rates, and macroeconomic indicators. Financial institutions use these simulations to estimate Value at Risk (VaR) and Unexpected Loss (UL), enhancing decision-making in risk management.
Modeling Retirement Planning Scenarios
Monte Carlo simulation models retirement planning by generating thousands of potential future market scenarios to estimate the probability of achieving financial goals. This technique incorporates variables such as investment returns, inflation rates, and life expectancy to assess portfolio longevity and withdrawal strategies under uncertain conditions. Financial advisors utilize these simulations to create personalized retirement plans that optimize asset allocation and reduce the risk of portfolio depletion.
Stress Testing Financial Models with Monte Carlo
Stress testing financial models with Monte Carlo simulation involves generating thousands of random scenarios for key risk factors such as interest rates, equity prices, and credit spreads to evaluate model robustness under extreme market conditions. By analyzing the distribution of possible outcomes, analysts can identify potential losses and vulnerabilities that traditional deterministic methods might overlook. This probabilistic approach enhances risk management frameworks, ensuring better preparation against market shocks and regulatory compliance.
Best Practices for Implementing Monte Carlo in Finance
Implementing Monte Carlo simulations in finance requires careful consideration of input data quality and distribution assumptions to ensure accurate risk assessment and portfolio optimization. Employ variance reduction techniques such as antithetic variates or control variates to enhance simulation efficiency and convergence speed. Rigorous validation through backtesting with historical data and sensitivity analysis helps validate model robustness and enhances decision-making confidence.
example of monte carlo in simulation Infographic
 samplerz.com
samplerz.com