In finance, Greeks refer to the various derivatives of an option's price with respect to underlying parameters. Delta measures the sensitivity of an option's price to changes in the price of the underlying asset. Gamma represents the rate of change of Delta relative to the underlying asset's price, indicating the curvature of the option's price. Vega quantifies the sensitivity of the option's price to changes in the volatility of the underlying asset. Theta measures the time decay of the option's value as it approaches expiration. Rho captures the sensitivity of the option's price to fluctuations in interest rates.
Table of Comparison
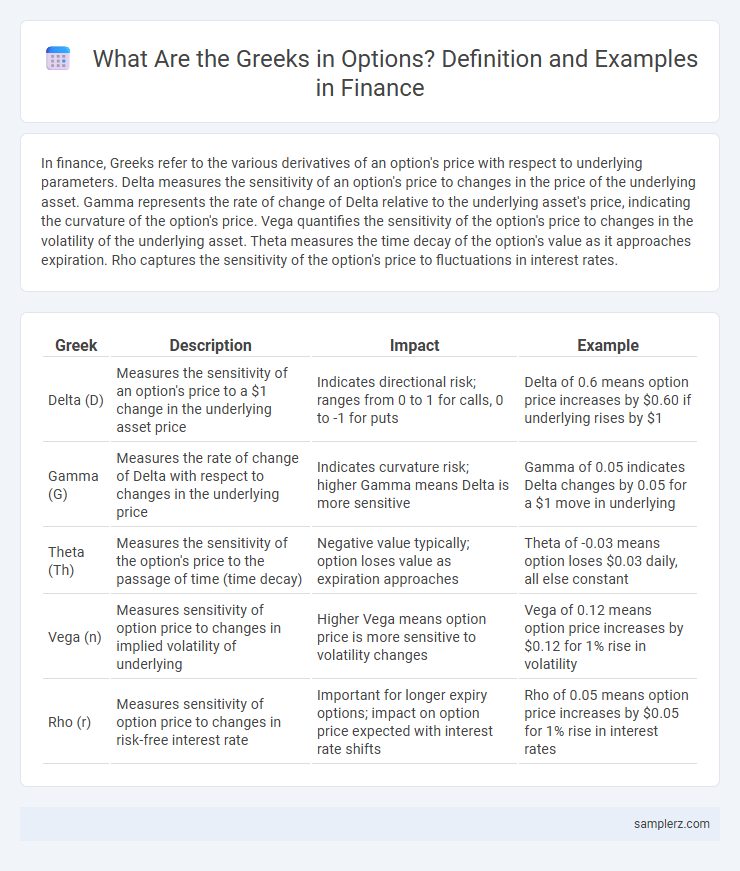
| Greek | Description | Impact | Example |
|---|---|---|---|
| Delta (D) | Measures the sensitivity of an option's price to a $1 change in the underlying asset price | Indicates directional risk; ranges from 0 to 1 for calls, 0 to -1 for puts | Delta of 0.6 means option price increases by $0.60 if underlying rises by $1 |
| Gamma (G) | Measures the rate of change of Delta with respect to changes in the underlying price | Indicates curvature risk; higher Gamma means Delta is more sensitive | Gamma of 0.05 indicates Delta changes by 0.05 for a $1 move in underlying |
| Theta (Th) | Measures the sensitivity of the option's price to the passage of time (time decay) | Negative value typically; option loses value as expiration approaches | Theta of -0.03 means option loses $0.03 daily, all else constant |
| Vega (n) | Measures sensitivity of option price to changes in implied volatility of underlying | Higher Vega means option price is more sensitive to volatility changes | Vega of 0.12 means option price increases by $0.12 for 1% rise in volatility |
| Rho (r) | Measures sensitivity of option price to changes in risk-free interest rate | Important for longer expiry options; impact on option price expected with interest rate shifts | Rho of 0.05 means option price increases by $0.05 for 1% rise in interest rates |
Introduction to Greeks in Options Trading
Delta measures the sensitivity of an option's price to changes in the underlying asset's price, indicating how much the option price moves per $1 change in the asset. Gamma represents the rate of change of delta with respect to the underlying price, highlighting the convexity of the option's value. Theta quantifies the time decay of the option, showing how much value the option loses as expiration approaches.
Delta: Measuring Price Sensitivity
Delta quantifies the sensitivity of an option's price to changes in the underlying asset's price, representing the rate of change in the option's premium for a one-unit move in the stock price. For example, a Delta of 0.5 indicates that the option's price will increase by $0.50 for every $1 rise in the underlying asset. This metric is crucial for traders managing risk and constructing hedging strategies in options portfolios.
Gamma: Assessing Delta’s Rate of Change
Gamma measures the rate of change of Delta relative to the underlying asset's price, providing critical insight into an option's sensitivity to market movements. A high Gamma value indicates that Delta will fluctuate significantly as the underlying asset's price changes, increasing the option's price responsiveness and risk exposure. Traders use Gamma to hedge portfolios more effectively and anticipate shifts in Delta during volatile market conditions.
Theta: Understanding Time Decay Effect
Theta represents the rate at which an option's value declines as expiration approaches, quantifying the time decay effect. It is expressed as a negative value indicating the loss an option incurs each day, with at-the-money options exhibiting the highest theta. Traders use theta to assess the risk of holding options positions over time, especially in strategies sensitive to time erosion.
Vega: Impact of Volatility on Option Prices
Vega measures the sensitivity of an option's price to changes in the underlying asset's volatility, indicating how much the option premium will increase or decrease with a 1% change in volatility. Higher Vega values are typically found in at-the-money options with longer time to expiration, reflecting greater exposure to volatility shifts. Understanding Vega is crucial for traders managing risk in volatile markets and optimizing option pricing strategies.
Rho: Interest Rate Influence on Options
Rho measures the sensitivity of an option's price to changes in interest rates, reflecting the impact of shifting rates on option valuations. For example, a call option on a stock tends to increase in value as interest rates rise, while a put option's value generally decreases. Traders use Rho to assess how fluctuations in the federal funds rate or Treasury yields influence their option strategies and risk management.
Practical Greek Calculations in Real Scenarios
Delta measures the sensitivity of an option's price to changes in the underlying asset's price, crucial for hedging strategies in volatile markets. Gamma assesses the rate of change of delta, helping traders adjust positions dynamically as the underlying price moves. Vega quantifies the impact of volatility shifts on option prices, essential for managing risk in earnings announcements or macroeconomic events.
Greeks Application in Hedging Strategies
Delta measures the sensitivity of an option's price to changes in the underlying asset, allowing traders to hedge by adjusting their stock positions accordingly. Vega gauges an option's sensitivity to volatility, helping hedge portfolios against fluctuations in market volatility. Gamma represents the rate of change of delta, enabling dynamic hedging by adjusting positions as the underlying price moves.
Visual Examples: Greeks in Action
Delta measures an option's sensitivity to changes in the underlying asset's price, with a delta of 0.5 indicating the option price moves half as much as the asset. Gamma represents the rate of change of delta, showing how delta shifts as the underlying price fluctuates, crucial for managing risk in rapidly changing markets. Vega quantifies the option's sensitivity to volatility, demonstrating how option premiums rise with increasing market uncertainty.
Key Takeaways for Greek Analysis in Options
Delta measures the sensitivity of an option's price to changes in the underlying asset's price, representing the hedge ratio for options portfolios. Gamma indicates the rate of change of delta, providing insight into potential risks as the underlying price moves. Vega quantifies the responsiveness of the option's price to volatility shifts, essential for managing exposure to market uncertainty.
example of greeks in option Infographic
 samplerz.com
samplerz.com