In finance, the Greeks represent key risk measures used in the analysis of derivatives, particularly options. Delta measures the sensitivity of an option's price to changes in the underlying asset's price, indicating how much the option's value will change with a one-unit move in the asset. Gamma quantifies the rate of change of delta with respect to the underlying asset's price, providing insight into the convexity of the option's value. Vega assesses the sensitivity of an option's price to changes in the volatility of the underlying asset, reflecting how option values shift as market uncertainty varies. Theta measures the time decay of an option, representing the decline in value as the expiration date approaches. Rho captures the sensitivity to changes in interest rates, showing the impact of monetary policy or market interest fluctuations on the option's price.
Table of Comparison
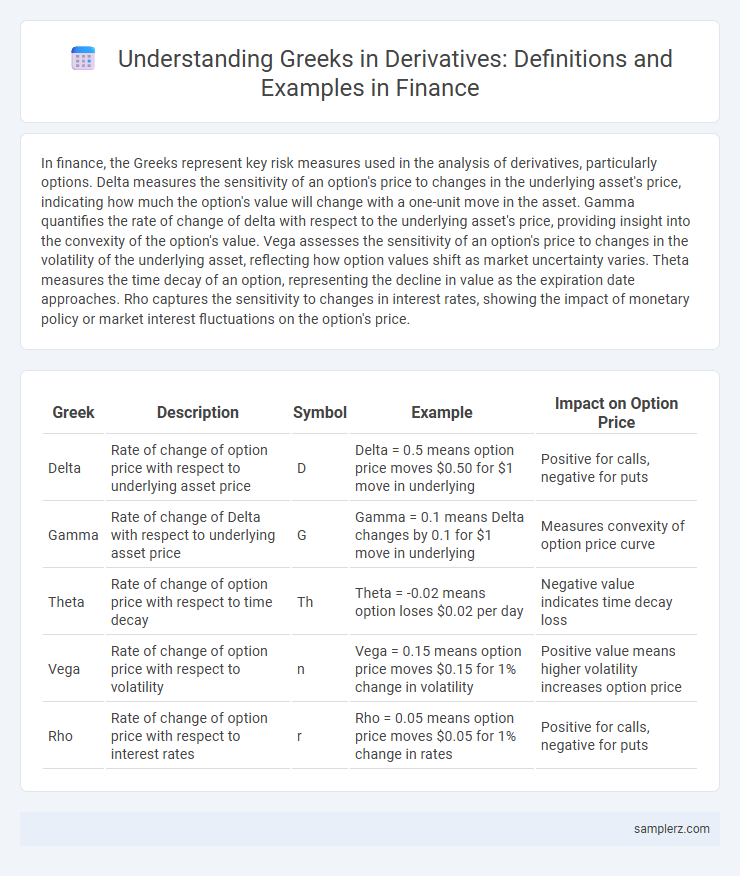
| Greek | Description | Symbol | Example | Impact on Option Price |
|---|---|---|---|---|
| Delta | Rate of change of option price with respect to underlying asset price | D | Delta = 0.5 means option price moves $0.50 for $1 move in underlying | Positive for calls, negative for puts |
| Gamma | Rate of change of Delta with respect to underlying asset price | G | Gamma = 0.1 means Delta changes by 0.1 for $1 move in underlying | Measures convexity of option price curve |
| Theta | Rate of change of option price with respect to time decay | Th | Theta = -0.02 means option loses $0.02 per day | Negative value indicates time decay loss |
| Vega | Rate of change of option price with respect to volatility | n | Vega = 0.15 means option price moves $0.15 for 1% change in volatility | Positive value means higher volatility increases option price |
| Rho | Rate of change of option price with respect to interest rates | r | Rho = 0.05 means option price moves $0.05 for 1% change in rates | Positive for calls, negative for puts |
Introduction to Greeks in Financial Derivatives
Greeks in financial derivatives quantify the sensitivity of options' prices to various underlying factors, essential for effective risk management and pricing strategies. Delta measures the rate of change in an option's price relative to movements in the underlying asset, while Gamma assesses the rate of change in Delta itself, indicating the curvature of price sensitivity. Vega represents sensitivity to volatility changes, Theta reflects time decay effects, and Rho evaluates sensitivity to interest rate fluctuations, collectively enabling traders to optimize portfolios under varying market conditions.
Delta: Measuring Price Sensitivity
Delta quantifies the sensitivity of an option's price to changes in the underlying asset's price, reflecting the expected change in option value for a one-unit movement in the stock price. For example, a delta of 0.6 indicates the option price will increase by $0.60 when the underlying asset rises by $1. This metric is crucial for hedging strategies and risk management in derivative portfolios.
Gamma: Assessing Delta’s Rate of Change
Gamma measures the rate of change of Delta in options trading, indicating how much Delta will shift as the underlying asset's price changes. A high Gamma value signals greater sensitivity, making option prices more responsive to small movements in the underlying stock. Traders use Gamma to manage risk and adjust positions, ensuring more precise hedging strategies in volatile markets.
Theta: The Effect of Time Decay
Theta quantifies the rate at which the value of an option decreases as time progresses, holding all else constant. This measure of time decay directly impacts option pricing, revealing how the option's premium erodes with each passing day. Traders closely monitor Theta to manage the diminishing extrinsic value of options, especially as expiration approaches.
Vega: Sensitivity to Volatility
Vega measures the sensitivity of a derivative's price to changes in the volatility of the underlying asset, reflecting the expected fluctuation magnitude. High Vega indicates significant price changes in options when volatility shifts, making it crucial for risk management and pricing strategies. Traders monitor Vega closely to hedge positions and capitalize on volatility movements in markets such as equities, commodities, and currencies.
Rho: Interest Rate Influence
Rho measures the sensitivity of a derivative's price to changes in interest rates, indicating how a 1% rise in interest rates impacts the option's value. For example, a call option on a stock may increase in value with rising rates due to higher cost of carry, while a put option typically decreases. Understanding Rho helps traders manage interest rate risk in portfolios containing options and other derivatives.
Real-World Example: Delta in Stock Options
Delta in stock options measures the sensitivity of an option's price to a $1 change in the underlying stock price, typically ranging between 0 and 1 for call options. For example, a call option with a delta of 0.6 implies the option price will increase by $0.60 if the underlying stock rises by $1. Traders use delta to hedge portfolios by adjusting their positions in the underlying stock, ensuring balanced risk exposure against price movements.
Calculating Greeks for a Call Option
Calculating Greeks for a call option involves determining Delta, Gamma, Theta, Vega, and Rho to measure sensitivity to underlying price, volatility, time decay, and interest rates. Delta quantifies the rate of change in the option's price relative to the underlying asset's price, while Gamma assesses the change in Delta itself. Vega evaluates sensitivity to volatility shifts, Theta reflects time decay impact, and Rho measures responsiveness to interest rate changes, essential for effective risk management in option portfolios.
Greeks in Risk Management Strategies
Delta measures the sensitivity of an option's price to changes in the underlying asset's price, serving as a primary risk indicator for directional exposure. Vega quantifies the impact of volatility fluctuations on the option's value, crucial for managing risks associated with market uncertainty. Gamma assesses the rate of change in delta, enabling dynamic hedging strategies that maintain portfolio stability under varying market conditions.
Interpreting Greeks in Portfolio Hedging
Delta measures the rate of change of a derivative's price relative to the underlying asset, guiding portfolio managers in adjusting positions to maintain desired risk exposure. Gamma assesses the stability of Delta, indicating potential portfolio shifts during significant market movements and informing dynamic hedging strategies. Vega quantifies sensitivity to volatility changes, enabling investors to hedge against fluctuations in market uncertainty and optimize portfolio resilience.
example of greeks in derivative Infographic
 samplerz.com
samplerz.com