Convexity in bonds measures the sensitivity of a bond's duration to changes in interest rates, providing a more accurate estimate of price fluctuations than duration alone. For example, a 10-year Treasury bond with a convexity of 120 will experience a larger price increase when interest rates fall and a smaller price decrease when interest rates rise, compared to a bond with lower convexity. This characteristic is crucial for investors managing interest rate risk and seeking to optimize portfolio returns. High convexity bonds tend to have higher premiums due to their beneficial price behavior during interest rate changes. Corporate bonds with embedded options, such as callable bonds, often exhibit lower convexity because the option limits price appreciation when rates decline. Understanding convexity helps financial analysts and portfolio managers improve bond valuation and risk assessment in dynamic interest rate environments.
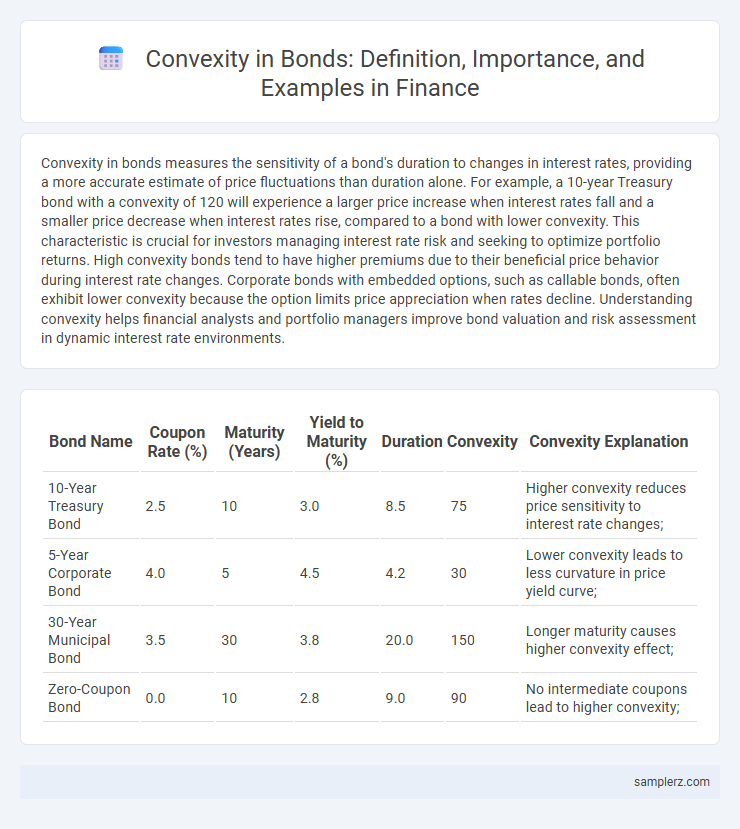
Table of Comparison
| Bond Name | Coupon Rate (%) | Maturity (Years) | Yield to Maturity (%) | Duration | Convexity | Convexity Explanation |
|---|---|---|---|---|---|---|
| 10-Year Treasury Bond | 2.5 | 10 | 3.0 | 8.5 | 75 | Higher convexity reduces price sensitivity to interest rate changes; |
| 5-Year Corporate Bond | 4.0 | 5 | 4.5 | 4.2 | 30 | Lower convexity leads to less curvature in price yield curve; |
| 30-Year Municipal Bond | 3.5 | 30 | 3.8 | 20.0 | 150 | Longer maturity causes higher convexity effect; |
| Zero-Coupon Bond | 0.0 | 10 | 2.8 | 9.0 | 90 | No intermediate coupons lead to higher convexity; |
Understanding Bond Convexity: Key Concepts
Bond convexity measures the curvature in the relationship between bond prices and yields, highlighting the sensitivity of a bond's duration to interest rate changes. High convexity indicates that bond prices increase more when yields fall and decrease less when yields rise, providing a cushion against interest rate volatility. This concept is essential for portfolio managers aiming to optimize bond returns while minimizing interest rate risk.
Why Convexity Matters in Bond Investing
Convexity measures the sensitivity of a bond's duration to changes in interest rates, capturing the curvature in the price-yield relationship. Higher convexity indicates that a bond's price will increase more when yields fall and decrease less when yields rise, reducing interest rate risk. Investors prioritize bonds with greater convexity to enhance portfolio stability and potentially achieve higher returns in volatile interest rate environments.
Real-World Example: Calculating Bond Convexity
Bond convexity measures the sensitivity of a bond's duration to changes in interest rates, providing a more accurate estimate of price fluctuations than duration alone. For example, consider a 10-year U.S. Treasury bond with a 3% coupon rate and a current yield of 2.5%; using bond convexity formulas, investors can calculate that a 1% drop in interest rates results in a price increase greater than predicted by duration, reflecting positive convexity. This calculation incorporates present values of future cash flows, weighted by the square of the time to payment, helping portfolio managers optimize risk and return in fixed-income investment strategies.
Convexity in Fixed-Rate Government Bonds
Convexity in fixed-rate government bonds measures the curvature of the relationship between bond prices and interest rates, providing a more accurate estimate of price changes than duration alone. For example, a 10-year U.S. Treasury bond exhibits positive convexity, meaning its price increases at an accelerating rate as yields decline, protecting investors from interest rate volatility. This characteristic is crucial for portfolio managers seeking to mitigate interest rate risk and enhance total return in a rising or falling rate environment.
Assessing Convexity with Callable Corporate Bonds
Callable corporate bonds exhibit negative convexity when rising interest rates increase the likelihood of the issuer not calling the bond, causing price sensitivity to deviate from standard convexity patterns. Assessing convexity in these bonds requires adjusting duration measures to account for embedded call options, which affect price volatility and yield changes. Accurate convexity analysis enables investors to better manage interest rate risk and optimize portfolio returns in the presence of call features.
Impact of Interest Rate Changes on Bond Convexity
Bond convexity measures the sensitivity of a bond's duration to changes in interest rates, reflecting how the bond's price accelerates as rates fluctuate. Higher convexity implies that when interest rates decline, bond prices increase more than predicted by duration alone, and when rates rise, prices decrease less drastically. This protective effect is crucial for managing interest rate risk, particularly in volatile markets where shifts can significantly impact portfolio value.
Comparing Duration and Convexity in Bonds
Duration measures a bond's price sensitivity to interest rate changes, estimating the approximate percentage change for small rate shifts. Convexity accounts for the curvature in the price-yield relationship, providing a more accurate price change estimate for larger interest rate movements. Comparing duration and convexity highlights that bonds with higher convexity experience less price decline when yields rise and more price appreciation when yields fall, improving risk management.
Portfolio Management: Leveraging Bond Convexity
Bond convexity enhances portfolio management by measuring the sensitivity of bond duration to interest rate changes, allowing managers to better predict price volatility and optimize bond selection. High-convexity bonds offer greater price appreciation potential during rate declines and reduced price depreciation during rate increases, improving portfolio risk-adjusted returns. Leveraging bond convexity helps in constructing resilient fixed-income portfolios that balance yield objectives with interest rate risk management.
Convexity Example in Zero-Coupon Bonds
Zero-coupon bonds exhibit higher convexity compared to coupon-bearing bonds due to the absence of intermediate interest payments, which causes their price to be more sensitive to interest rate changes. For example, a zero-coupon bond with a 10-year maturity experiences larger price increases when yields fall, reflecting greater convexity effects. This increased convexity leads to more pronounced price volatility, making zero-coupon bonds important instruments for interest rate risk management and portfolio immunization strategies.
Risk Mitigation Using Bond Convexity
Bond convexity measures the sensitivity of a bond's duration to interest rate changes, providing a more accurate estimate of price fluctuations than duration alone. By incorporating convexity into risk assessment, investors can better anticipate bond price volatility and reduce interest rate risk in their portfolios. This enhanced risk mitigation strategy helps optimize bond portfolio performance during varying interest rate environments.
example of convexity in bond Infographic
 samplerz.com
samplerz.com