Bootstrapping in finance refers to the method used to construct a zero-coupon yield curve from the prices of a series of coupon-bearing bonds. This technique extracts spot rates for different maturities by sequentially solving for the discount factors implied by bond prices. The process starts with the shortest maturity bond and iteratively derives longer-term rates, ensuring the yield curve reflects current market conditions without arbitrage opportunities. A practical example involves using Treasury securities data, where the yield on a 3-month T-bill is directly observed as the first spot rate. The next step calculates the spot rate for a 6-month bond by adjusting for the interest accrued from the 3-month rate, followed by solving for the 1-year rate using the 6 and 12-month bond prices. This approach allows accurate derivation of zero-coupon yields essential for valuing derivatives, managing interest rate risk, and performing fixed-income portfolio analysis.
Table of Comparison
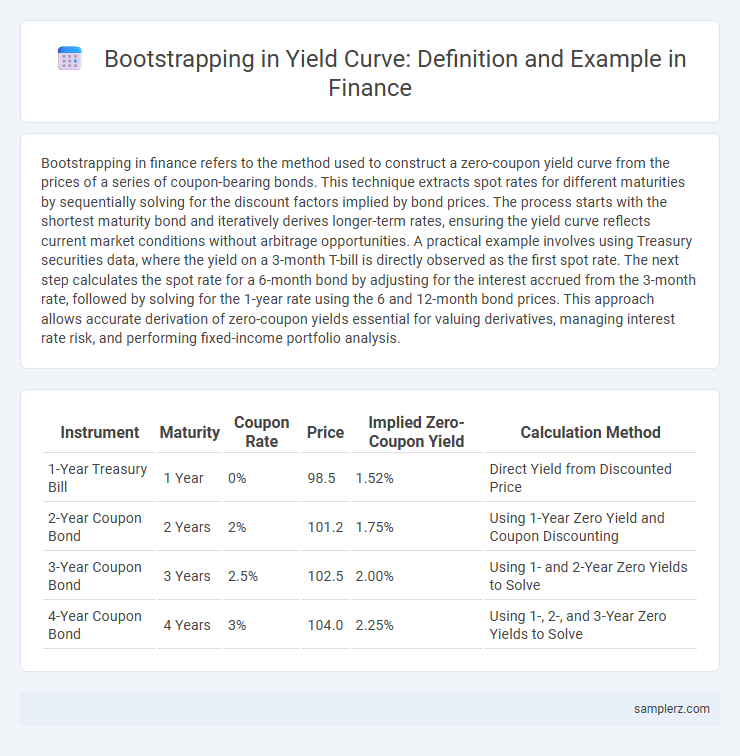
| Instrument | Maturity | Coupon Rate | Price | Implied Zero-Coupon Yield | Calculation Method |
|---|---|---|---|---|---|
| 1-Year Treasury Bill | 1 Year | 0% | 98.5 | 1.52% | Direct Yield from Discounted Price |
| 2-Year Coupon Bond | 2 Years | 2% | 101.2 | 1.75% | Using 1-Year Zero Yield and Coupon Discounting |
| 3-Year Coupon Bond | 3 Years | 2.5% | 102.5 | 2.00% | Using 1- and 2-Year Zero Yields to Solve |
| 4-Year Coupon Bond | 4 Years | 3% | 104.0 | 2.25% | Using 1-, 2-, and 3-Year Zero Yields to Solve |
Introduction to Bootstrapping in Yield Curve Construction
Bootstrapping in yield curve construction involves sequentially deriving zero-coupon rates from the prices of coupon-bearing bonds to create a complete yield curve. By isolating the spot rates for each maturity, this method enables accurate discount factor calculations essential for valuing various fixed income securities. The step-by-step extraction of zero rates ensures the yield curve reflects true market conditions and supports precise interest rate risk management.
Key Concepts Behind Yield Curve Bootstrapping
Yield curve bootstrapping involves constructing a zero-coupon yield curve from the prices of coupon-bearing bonds by sequentially solving for spot rates. This method relies on the principle that the yield of longer maturity bonds can be inferred once shorter maturity spot rates are known, enabling accurate discount factor extraction. Key concepts include using market prices, coupon payments, and iterative calculations to derive spot rates at successive maturities, which facilitate precise valuation and risk management in fixed income markets.
Step-by-Step Example of Bootstrapping Yield Curve
To bootstrap a yield curve, begin by using short-term instruments such as overnight rates or Treasury bills to derive the initial spot rates. Next, calculate the discount factors for these maturities and apply them sequentially to longer-term instruments like notes or bonds, ensuring each spot rate is determined from previously computed discount factors. Finally, iteratively solve for the spot rates at successive maturities by equating the present value of future cash flows to the observed market prices, constructing a full, arbitrage-free yield curve.
Required Market Data for Bootstrapping
Bootstrapping the yield curve requires precise market data, including spot rates from zero-coupon bonds, prices of coupon-bearing bonds, and forward rates derived from swap rates. Accurate inputs such as bid-ask spreads, bond maturities, and coupon frequencies are essential to construct a reliable zero-coupon yield curve. High-quality data from liquid government securities and well-traded corporate bonds enhances the accuracy of bootstrapped discount factors and forward rate estimations.
Bootstrapping Zero-Coupon Yield Curve: Practical Illustration
Bootstrapping zero-coupon yield curves involves deriving spot rates from the prices of coupon-bearing bonds by sequentially solving for each maturity's zero rate, ensuring that the present value of cash flows matches observed market prices. For example, starting with short-term maturities like 6-month Treasury bills, the process extracts the zero-coupon rate directly from the price, then uses these rates to discount subsequent bond cash flows sequentially, revealing zero rates for longer terms. This method results in a continuous spot rate curve essential for accurately pricing interest rate derivatives and managing bond portfolio risks.
Calculating Spot Rates Using Bootstrapping
Calculating spot rates using bootstrapping involves deriving zero-coupon yields from the prices of coupon-bearing bonds by sequentially solving for each maturity's spot rate. This method starts with the shortest maturity bond, extracting its spot rate directly, then uses these rates to discount future cash flows of longer maturity bonds, isolating unknown spot rates iteratively. Bootstrapping enables precise construction of the yield curve, essential for accurate valuation of fixed-income securities and risk management.
Deriving Forward Rates from Bootstrapped Yield Curve
Bootstrapping in yield curve construction involves deriving zero-coupon rates from a set of coupon-bearing bond prices to establish a consistent zero-coupon yield curve. Forward rates are then calculated using these zero rates, reflecting the market's expectations of future interest rates, critical for pricing derivatives and managing interest rate risk. This method ensures accurate valuation of financial instruments by linking spot rates to implied future rates through iterative calculations.
Applications of Bootstrapped Yield Curves in Finance
Bootstrapped yield curves are essential in pricing fixed income securities, enabling accurate discount factor extraction for cash flow valuation. Financial institutions utilize these curves to benchmark interest rates, assess credit risk, and execute interest rate swaps effectively. Portfolio managers rely on bootstrapped curves to optimize asset-liability matching and enhance risk-adjusted returns.
Limitations and Considerations in Bootstrapping Process
Bootstrapping a yield curve involves deriving zero-coupon rates from observed market prices of bonds, but it faces limitations such as sensitivity to data quality and market liquidity, which can lead to inaccuracies in the curve construction. The presence of bid-ask spreads and infrequent trading reduces the reliability of input prices, causing distortions in the derived discount factors. Considerations include ensuring a wide range of maturities, smoothing techniques to handle non-parallel shifts, and adjusting for credit risk to improve the robustness of the bootstrapped yield curve.
Conclusion: Benefits of Bootstrapping Yield Curves
Bootstrapping yield curves enables precise estimation of zero-coupon rates from market data, improving accuracy in bond pricing and risk management. This method enhances the ability to value various fixed-income securities by producing a smooth, arbitrage-free yield curve. Financial analysts benefit from improved model calibration and more informed investment decisions using bootstrapped curves.
example of bootstrapping in yield curve Infographic
 samplerz.com
samplerz.com