In cryptography, a common example of the pigeonhole principle occurs in hash functions. A hash function generates fixed-size outputs from variable-length inputs, meaning the number of possible inputs exceeds the number of possible outputs. This disparity guarantees that two different inputs will produce the same hash value, known as a collision. Collision resistance is a critical property in cryptographic hash functions, yet the pigeonhole principle ensures that collisions cannot be entirely avoided. This inherent limitation drives security researchers to design functions that minimize collision chances and make finding them computationally infeasible. Practical applications include digital signatures and data integrity verification, where hash collisions could undermine security.
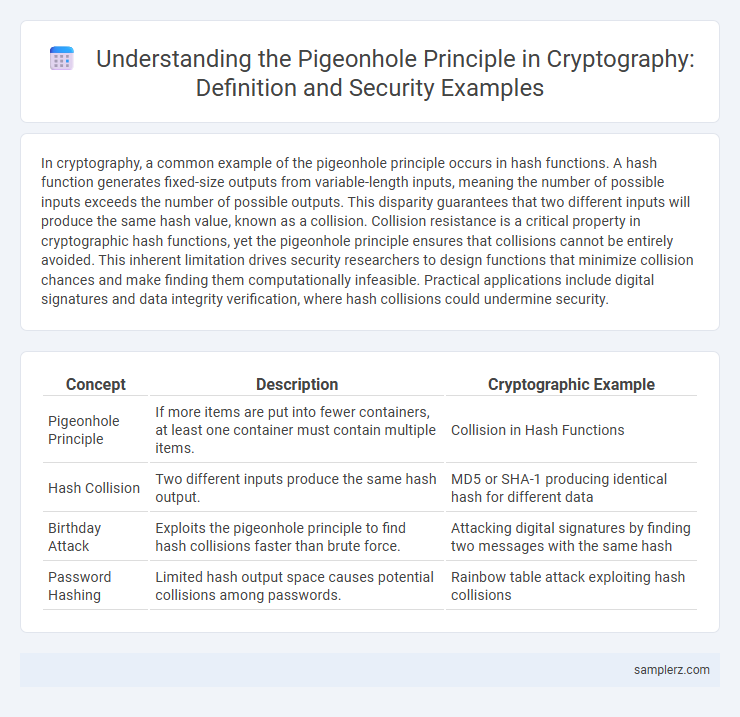
Table of Comparison
| Concept | Description | Cryptographic Example |
|---|---|---|
| Pigeonhole Principle | If more items are put into fewer containers, at least one container must contain multiple items. | Collision in Hash Functions |
| Hash Collision | Two different inputs produce the same hash output. | MD5 or SHA-1 producing identical hash for different data |
| Birthday Attack | Exploits the pigeonhole principle to find hash collisions faster than brute force. | Attacking digital signatures by finding two messages with the same hash |
| Password Hashing | Limited hash output space causes potential collisions among passwords. | Rainbow table attack exploiting hash collisions |
Understanding the Pigeonhole Principle in Cryptography
The pigeonhole principle in cryptography highlights that when encrypting more messages than available ciphertexts, collisions are inevitable, leading to potential vulnerabilities. Hash functions, such as SHA-256, illustrate this concept by mapping infinite inputs into a fixed-size output, making hash collisions a critical concern for data integrity. Understanding this principle helps cryptographers design algorithms that minimize collision risks, ensuring stronger encryption and secure communication.
Classical Cryptographic Attacks Leveraging the Pigeonhole Principle
Classical cryptographic attacks leveraging the pigeonhole principle exploit the fact that when a large set of inputs is mapped into a smaller set of outputs, collisions are inevitable. A notable example is the birthday attack on hash functions, where finding two different inputs producing the same hash value drastically reduces the complexity of breaking the system. This principle underpins collision attacks in cryptographic algorithms like MD5 and SHA-1, highlighting vulnerabilities in their hash output size.
Real-World Examples: Pigeonhole Principle and Password Cracking
The pigeonhole principle demonstrates vulnerabilities in password security by illustrating that limited password lengths and character sets force multiple users to share potential password hashes, enabling attackers to exploit hash collisions in real-world cracking scenarios. For example, rainbow tables utilize this principle by precomputing hash values to rapidly reverse-engineer passwords, making systems with weak hashing algorithms especially susceptible. Organizations mitigate these risks by implementing complex password policies and strong cryptographic hash functions like bcrypt or Argon2, significantly reducing collision chances and enhancing overall security.
Vulnerabilities in Hash Functions: Insights from the Pigeonhole Principle
The pigeonhole principle reveals fundamental vulnerabilities in hash functions by demonstrating that collisions are inevitable when mapping a large input space to a fixed-size output. This principle underscores risks in cryptographic hash functions such as MD5 and SHA-1, where attackers exploit collision attacks to compromise data integrity and authentication. Understanding these vulnerabilities helps security professionals develop stronger cryptographic algorithms resistant to collision-based exploits.
Pigeonhole Principle in Birthday Attacks
The Pigeonhole Principle underpins Birthday attacks by exploiting the probability of hash collisions within a fixed output space. In cryptography, when hashing n inputs into m possible outputs where n > m, the principle guarantees that at least two inputs share the same hash, enabling attackers to find collisions more efficiently than brute force. This vulnerability is critical in hash functions like MD5 and SHA-1, which have relatively small hash sizes compared to the vast number of possible inputs.
Analyzing Digital Signatures through the Pigeonhole Lens
Analyzing digital signatures through the pigeonhole principle reveals vulnerabilities in hash functions, where a limited output space forces collisions between different inputs, compromising signature integrity. Attackers exploit these collisions to forge signatures by finding two distinct messages that produce the same hash, undermining authentication and non-repudiation. Understanding the pigeonhole principle in this context is critical for designing secure cryptographic algorithms resistant to collision attacks.
Block Cipher Weaknesses: The Role of the Pigeonhole Principle
Block cipher weaknesses often arise from the pigeonhole principle, which states that when more plaintext blocks than possible ciphertext blocks exist, collisions are inevitable. This principle underpins attacks like the birthday attack, where repeated ciphertexts reveal patterns and reduce effective key space. Understanding these collisions enables cryptanalysts to exploit vulnerabilities in block cipher modes such as ECB, compromising data confidentiality.
Securing Communication Protocols Against Pigeonhole Exploits
Pigeonhole attacks exploit deterministic patterns in cryptographic protocols, allowing attackers to correlate encrypted messages with specific data by limiting possible outputs. Securing communication protocols involves incorporating randomized padding and probabilistic encryption schemes to obscure data patterns and prevent message repetition analysis. Implementing these defenses strengthens confidentiality and mitigates vulnerabilities inherent in predictable cryptographic operations.
Designing Cryptographic Algorithms to Mitigate Pigeonhole Risks
Designing cryptographic algorithms to mitigate pigeonhole risks involves ensuring that the output space is sufficiently large to prevent collisions, as pigeonhole principle implies that smaller output spaces than input domains inevitably lead to identical outputs. Techniques such as increasing hash output length, employing random salts, and using iterative compression functions reduce the probability of collisions and enhance cryptographic strength. Robust algorithm design considers these factors to maintain data integrity and resist collision-based attacks like birthday attacks.
Future Trends: Advances Addressing Pigeonhole-Based Threats
Emerging quantum-resistant algorithms leverage lattice-based cryptography to counter pigeonhole principle vulnerabilities by ensuring that hash outputs remain collision-resistant against quantum attacks. Research into homomorphic encryption enhances data security without sacrificing functionality, mitigating risks of hash collisions in encrypted environments. Continuous development in error-correcting codes and hash function diversification further strengthens defense mechanisms against pigeonhole-based breaches.
example of pigeonhole in cryptography Infographic
 samplerz.com
samplerz.com